자료구조의 종류와 특징에 대해 간단히 알아보자.
- 자료구조의 정의
- 자료구조의 종류
- 시간 복잡도
1. 자료구조
- 정의
데이터를 저장, 조직화, 관리, 처리하는 방법을 정의한 것
자료구조는 효율적인 알고리즘을 구현하기 위해 반드시 필요하다. 해결해야 하는 문제에 따라 적절한 자료구조를 선택하는 것이 성능에 직접적인 영향을 미친다.
- 종류와 특징
(1) 배열
동일한 자료형의 데이터를 연속된 메모리에 저장하는 구조
- 장점 : 인덱스를 이용한 빠른 접근이 가능함.
- 단점 : 크기가 고정됨. 삽입 및 삭제 비용이 큼.
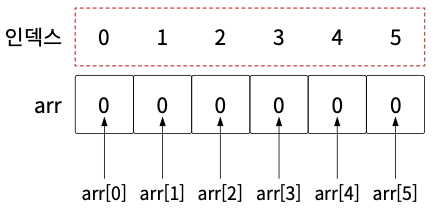
예) 정렬과 관련된 알고리즘, 이차원 배열을 활용한 행렬 등
(2) 연결 리스트
각 노드가 데이터 + Pointer 를 함께 저장하는 구조
단일 / 이중 / 원형으로 총 세가지 종류가 있음.
- 장점 : 삽입 및 삭제에 유리함. 메모리 낭비가 없음.
- 단점 : 인덱스를 통한 접근 불가. 캐시가 비효율적.
※ Pointer : 다음 노드의 주소

예) 메모리 할당 관리, 힙 구현, Undo/Redo 기능 등
(3) 스택
후입선출 방식의 자료구조
스택에는 마지막으로 삽입된 데이터가 먼저 제거된다.
- push : 데이터 삽입 연산
- pop : 데이터 제거 연산
- peek : 최상단 데이터 조회 연산
- 장점 : 구조가 단순함. 구현이 용이함.
- 단점 : 중간 요소에 접근 불가능.

예) 재귀 함수 호출, 괄호 검사, 웹브라우저의 뒤로가기 등
(4) 큐
선입선출 방식의 자료구조
큐에서는 먼저 들어온 데이터가 먼저 나가게 된다. 큐는 변형된 형태로도 사용이 가능하다.
- 원형 큐
- 덱(Deque) - 양쪽에서 삽입/삭제 가능
- 우선순위 큐
- 장점 : 순차적인 작업 처리에 유리함.
- 단점 : 일반 큐는 크기를 고정할 시 오버플로우 발생 가능.

예) CPU 작업 스케줄링, 프린터의 작업 큐, BFS 탐색 등
(5) 해시 테이블
데이터를 키-값 쌍으로 저장하는 자료구조
해시 테이블에서는 키를 해시 함수에 넣어서 인덱스를 계산한다. 평균적으로 탐색 속도가 매우 빠르지만, 해시 충돌을 해결해야한다.
- 장점 : 빠른 검색 / 삽입 / 삭제
- 단점 : 충돌 발생 시 성능 저하. 해시 함수의 설계가 중요함.

예) 데이터베이스 인덱스, 캐시 구현, 중복 제거 등
(6) 트리
계층 구조를 이루는 비선형 자료구조
루트(기반) 노드부터 시작해서 아래로 뻗어나가는 자식 노드가 존재한다. 트리는 아주 많은 종류로 나눌 수 있는데, 대표적으로 다음과 같은 트리가 있다.
- 이진트리, 이진 탐색 트리
- 힙, AVL 트리, 레드-블랙 트리
- 트라이, 세그먼트 트리
- 장점 : 정렬된 데이터 저장에 유리함.
- 단점 : 구현이 복잡하고 균형 유지가 필요함.

예) 이진 탐색, 힙 정렬, 데이터베이스 인덱스, 파일 시스템 구조 등
(7) 그래프
정점과 간선으로 구성된 자료구조
그래프는 정점과 정점 사이의 연결관계를 표현하고 있다. 그래프는 방향과 가중에 따라 나눌 수 있다.
- 방향 그래프 / 무방향 그래프
- 가중 그래프 / 비가중 그래프
그래프를 표현하는 방법에는 인접 리스트 / 인접 행렬의 방법이 있다.
- 장점 : 관계의 표현에 유리함 (네트워크, 소셜 등)
- 단점 : 구현이 복잡하고 탐색 비용이 큼.

예) 소셜 네트워크, 지도 앱의 길 찾기 기능, 그래프 알고리즘 등
2. 시간 복잡도
- 정의
입력크기에 따라 알고리즘이 수행하는 연산 횟수 혹은 실행 시간의 증가 정도를 표현한 척도
시간 복잡도를 계산하는 것은 입력이 커질수록 알고리즘이 얼마나 더 느려지는지를 분석하는 것이다. 보통 빅오 표기법을 사용해서 시간 복잡도를 표현한다.
시간 복잡도는 정확한 시간을 나타내는 것이 아닌, 성능 추세를 보는 개념이라고 이해하면 된다.
- 빅오 표기법
| 시간 복잡도 | 이름 | 설명 |
| O(1) | 상수 시간 | 입력 크기와 상관없이 항상 일정한 시간 |
| O(log n) | 로그 시간 | 입력이 커질수록 증가 속도가 느림 (예 : 이진 탐색) |
| O(n) | 선형 시간 | 입력이 늘어나면 실행 시간도 비례해서 증가 |
| O(n log n) | 로그 선형 시간 | n 보다 느리지만 n^2 보다는 빠름 (예 : 병합 정렬) |
| O(n^2) | 이차 시간 | 이중 반복문에서 주로 나타나는 시간 (예 : 버블 정렬) |
| O(2^n) | 지수 시간 | 입력이 조금만 커져도 급격히 느려짐 (예 : 모든 조합 탐색) |
| O(n!) | 팩토리얼 시간 | 가능한 모든 순열을 탐색 (예 : 외판원 문제) |
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ) < O(n!)
- 자료구조별 시간 복잡도
| 자료구조 | 접근 | 탐색 | 삽입 | 삭제 |
| 배열 | O(1) | O(n) | O(n) | O(n) |
| 연결 리스트 | O(n) | O(n) | O(1)* | O(1)* |
| 스택 | O(n) | O(n) | O(1) | O(1) |
| 큐 | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블 | - | O(1)* | O(1)* | O(1)* |
| 이진 탐색 트리 | O(log n)* | O(log n)* | O(log n)* | O(log n)* |
| 그래프(인접 리스트) | - | O(V + E) | O(1) | O(1) |
| 그래프(인접 행렬) | - | O(V^2) | O(1) | O(1) |
* : 최적 / 평균적인 경우
해시 테이블의 경우 충돌이 많이 발생하면 O(n) 까지 떨어질 수 있다. 트리는 균형이 잡힌 상태를 유지해야 O(log n) 의 시간 복잡도를 보장할 수 있다.
< 출처 >
https://www.boardinfinity.com/blog/graphs-in-data-structure/
'CS' 카테고리의 다른 글
| 2.운영체제 (2) - 운영체제의 관리 작업 (0) | 2025.03.07 |
|---|---|
| 2. 운영체제 (1) - 운영체제의 구성과 역할 (0) | 2025.03.04 |
| 1. 컴퓨터 구조 (2) - CPU / 메모리 / 보조기억장치 / 입출력 장치 (0) | 2025.02.27 |
| 1. 컴퓨터 구조 (1) - 데이터 / 명령어 (0) | 2025.02.26 |
| CS 학습 로드맵 (0) | 2025.02.25 |